More than just a pretty space: how symmetry hides in science

For most people, the word “symmetry” evokes memories of making paper snowflakes or learning about isosceles triangles in their high school. So quite often When I tell peers that my research involves symmetry, the most common reaction is to ask “Why are you interested in a subject like this?” or “What relevance does this have to the modern world?”. This article is here to address these questions and so that we can explore symmetry beyond the classroom!
To mathematicians, the word symmetry makes us think of a type of maths called ‘Group Theory’. Group Theory is one of the oldest active areas of mathematical research, originating from the same Islamic scholars that pioneered modern algebra. This isn’t surprising, if one were to look at the beautiful mandalas or intricate tiling systems found across the Islamic world; people were interested in symmetry in the medieval period!

By the mid 19th Century, people had noticed that the symmetry of objects could be associated with a mathematical object which came to be known as a “group”. Since then, a lot of progress has been made from studying these “groups”. For example, mathematicians have classified all finite ‘simple’ groups, an achievement akin to writing the periodic table for symmetries—all other finite simple groups are made of these. This was not an easy job. Hence, it has been argued as being the most complicated result in all of modern mathematics, developed by over 100 mathematicians with a proof covering approximately 10,000 pages (more than eight times longer than the Bible). 1
Even so, the picture is still far from clear. There are many groups which are “infinite” in the sense that they have infinitely many different moves you can make– like the symmetry of a circle or sphere. This is a good thing too, otherwise I would be out of a job!
What makes symmetry so mysterious is that we can think of the symmetry of all kinds of strange objects. Consider the symmetry of a Rubik’s cube. Not only can we rotate the entire shape, but also rotate isolated parts of it in an incomprehensibly huge number of ways—we could say that this is also a “type” of symmetry. This rich history and elusive nature makes it incredibly alluring to mathematicians, who love abstract problems that arise naturally within anyone who has an inquisitive mind.

However, abstract questions generally get a bad reputation. Anyone who has ever been in a maths lesson has heard the all important question “How will we ever use this in the real world?”. The beauty of answering abstract questions is that then your work becomes useful in all kinds of weird and wonderful places which you might never have thought. Symmetry is no exception. Below, I give six of my favourite examples…
Virology
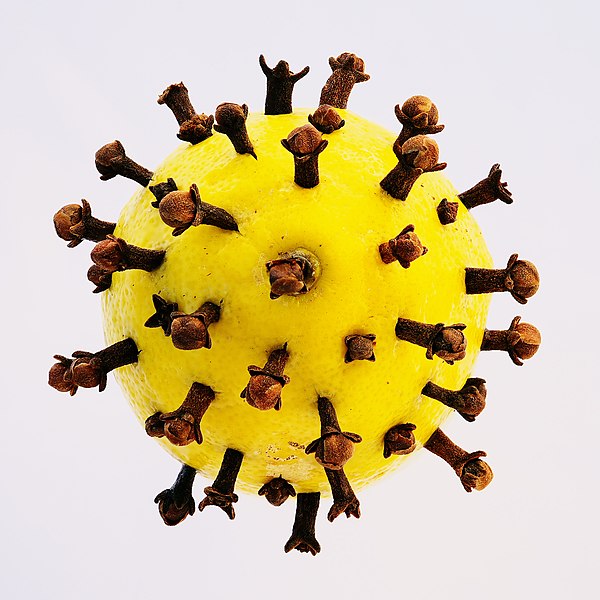
That’s right, symmetry is crucial to understanding viruses such as the one that causes the disease COVID-19. Some of the ways in which we classify viruses and are able to identify new strains of commonly known viruses is by analysing their symmetries—through NMR (nuclear magnetic resonance) spectroscopy, X-ray crystallography, and electron microscopy we can associate different groups with different viruses depending on their shape. The type of symmetries we find can correspond to important factors such as transmissibility and half life. 2
Theoretical Physics

Modern theoretical physics relies very heavily on the study of ‘Lie Groups’.3 They encode the symmetries of many physical problems. A widely espoused example of this is that analysis of the Schrödinger equation, which can be thought of as “the modern version of F=ma”, can be hugely simplified by using the theory of ‘Lie Groups’.4 This makes physics easier, and helps us understand small scale particle physics, for example.
Chemistry
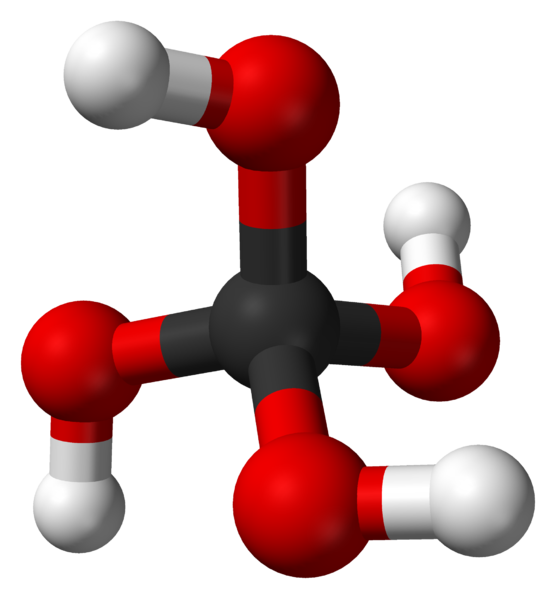
Colour code: Carbon, C: grey-black, Oxygen, O: red, Hydrogen, H: white
‘Group Theory’ is fundamental to Chemistry—anyone with a bachelor’s degree in Chemistry will learn what a symmetry point group is. The reason for this is one way in which we identify different molecules is via their point group—the different types of symmetries which leave it unchanged. Molecules can have very complicated symmetry point groups, with many axes of rotation and mirror symmetries, therefore group theory can help you understand what molecules you are looking at. 5
Material Science

Some materials are stronger than others—you wouldn’t make an umbrella out of paper or a teapot out of chocolate. The strongest materials have a lot of interesting symmetries—think of diamond, for example. Material scientists have found ways to quantify the strength of materials using group theory, and used this to investigate important materials we use everyday such as carbon nanotubes for bicycles and graphene for pencils.
Digital Security

It is perhaps unsurprising that our internet security relies on’Group Theory’.6 In ‘Group Theory’, many problems which are hard to solve are easy to verify, if we have a solution. For example, consider the Rubik’s cube—if someone proposes a certain set of moves that would solve the puzzle, it would not take long to check. However, if the same person asked you to check every possible move, this would take much longer!
Modern cryptography relies on these sorts of problems in order to keep your money and private messages safe. By associating a password with a certain sequence of moves on a Rubik’s cube, you can be let in quickly – even on your iPhone. Meanwhile (?)someone trying to hack you on a very powerful computer would still struggle to check through all the passwords.
Beauty
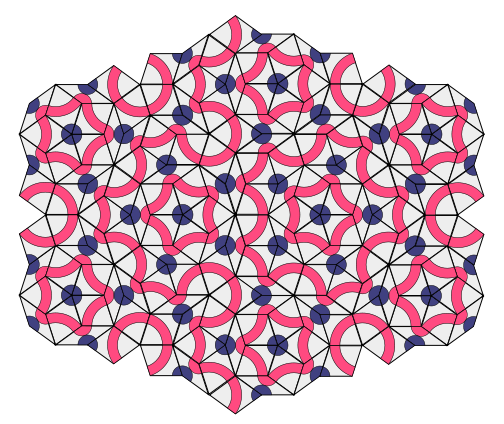
Besides being useful and interesting, symmetry has remained important globally in creating architecture, design and art. This led the mathematician Ian Stewart to call Group Theory, “the study of beauty”.
Perhaps this is the real reason so many mathematicians dedicate their lives to symmetry, because it allows us to spend time indulging in some of the most intricate, elegant and inherently beautiful work humans have ever done.
The author cites a book entitled “Why Beauty is Truth: The History of Symmetry” by Ian Stewart (Amazon)
This article was specialist edited by Richard Murchie and copy-edited by Holly Leslie
References
- https://plus.maths.org/content/enormous-theorem-classification-finite-simple-groups
- https://www.onlinebiologynotes.com/virus-structure-symmetry/
- https://aimath.org/E8/liegroup.html
- https://iopscience.iop.org/article/10.1088/0143-0807/34/5/1175
- https://symotter.org/gallery
- https://en.wikipedia.org/wiki/Group-based_cryptography









