The Tortoise and the Mathematician: A Tale of Geometry

The Gömböc (pronounced gumboots): a shape with unique mechanical properties, and a surprisingly diverse range of applications1. The shape defies friction and geometry by only having two places it will rest – one stable and the other not. A body with these properties is called a mono-monostatic body, and these two positions are known as its equilibrium points.
The shape, discovered in 2006 by Gabor Domokos and Péter Várkonyi – both at the Budapest University of Technology and Economics, Hungary, was the result of an attempt to prove a conjecture posed in 1995 by Russian mathematician Vladimir Arnold. The conjecture was that ‘convex homogeneous bodies with less than four equilibrium points may exist’. This may initially seem overbearing with its mathematical terminology, so let’s deconstruct it.
If something is convex then it doesn’t curve inwards at any point of the shape; an egg is convex, whereas an hourglass isn’t (instead it’s concave). If something is homogeneous then it’s made from a uniform material with equal density throughout.
An equilibrium point is a place of balance; for instance, a stable equilibrium point would be the base of a triangular pyramid. It is also where the distance between the centre of gravity (G) and the boundary of the shape is at a minimum (its local minimum). An example of an unstable equilibrium point (where even a small perturbation causes the body to move from that point) would be the tip of a pencil. An unstable equilibrium point is where the distance between G and the boundary of the shape is at a maximum (its local maximum). The natural equilibrium points of an object are determined by the position of its centre of mass and its geometry.
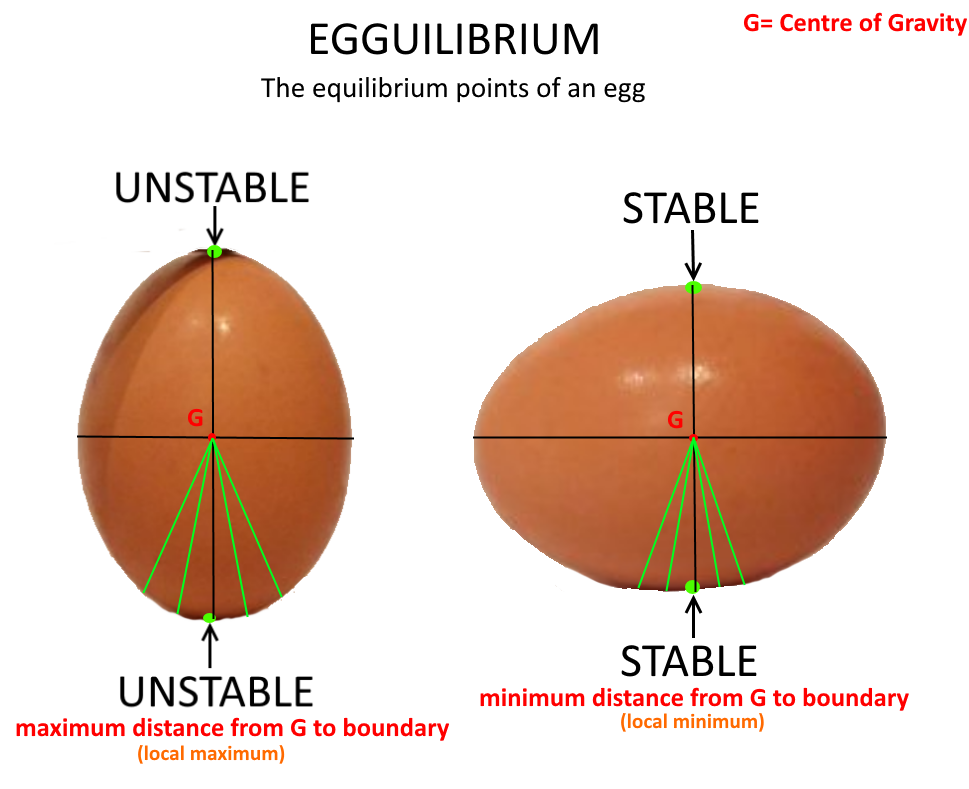
The equilibrium points of an egg
Mathematicians knew that a Gömböc couldn’t exist in 2D. Any less than four equilibrium points in a homogeneous convex 2D body would create impossible demands on its G, and the Gömböc only has two equilibrium points.
Imagine a 2D shape that only has one stable, and one unstable equilibrium point. G has to simultaneously be closest to the stable equilibrium point, and furthest from the unstable equilibrium point. If it was in that position, you could split the shape into two parts with G lying on the line separating them: one part being small while containing the stable equilibrium point (local minimum), and one larger part containing the unstable equilibrium point (local maximum). A contradiction arises, G should lie in the larger of the two sides due to the heavier nature of the larger part. Thus G can’t be on this line. Local minima follow local maxima: this means the number of stable and unstable equilibria must be equal in 2D. The contradiction and the equality of different types of equilibria prove that four is the minimum number of equilibrium points in 2D2.
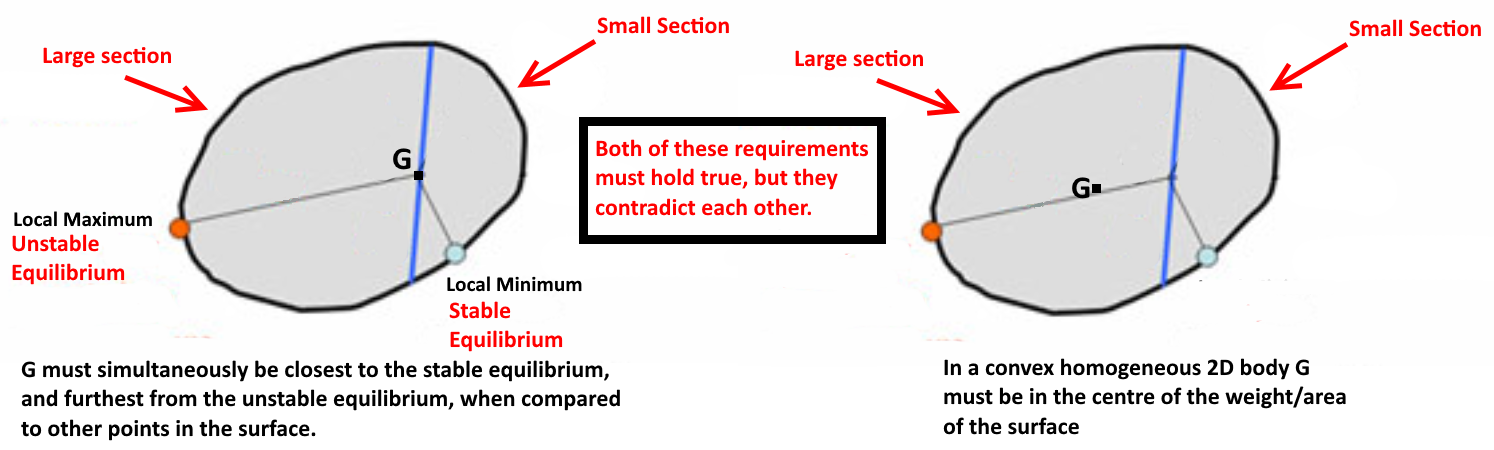
The centre of gravity contradiction that arises with a hypothetical 2D Gömböc
In the third dimension, another type of equilibrium point is possible: the saddle point. If pushed, this position is stable in one direction but unstable in all other directions. For convex and homogeneous 3D shapes, there is a relationship that dictates how many saddle points there are. Take S to be a stable equilibrium point, U to be an unstable equilibrium point, T=S+U-2 gives the number of saddle points (T). Proven mathematically by the Poincaré-Hopf Theorem. The saddle point relationship opens the possibility of a Gömböc in 3D, as one S and one U would mean there is no saddle point (T) present, thus meaning there are only two equilibrium points in total.
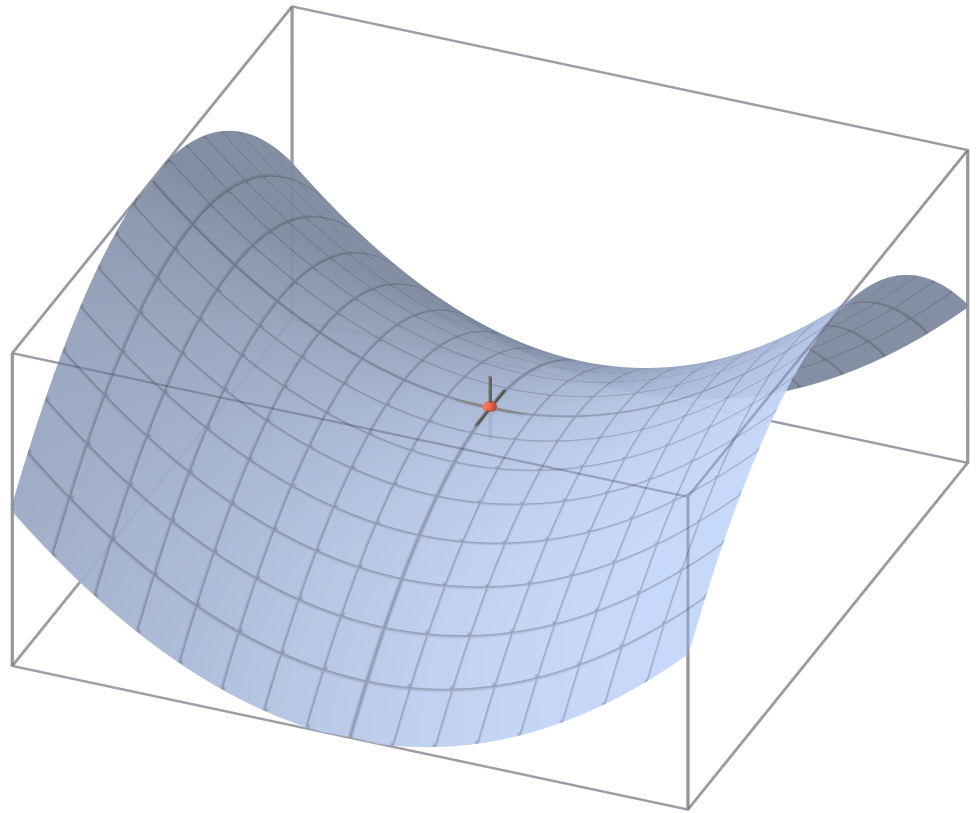
Visualisation of a saddle point
From the saddle point relationship, Domokos started to classify objects by their equilibrium configuration, a value given by (S, U, T). Domokos began with simple examples; the cube has six S points (the centre of each face), eight U points (each corner/vertex), and 12 T points (the centre of each side). They came to the realisation that it is easy to add another equilibrium point by making a calculated deformation, but it is hard to remove an equilibrium point. The ability to derive other shapes from a simpler one by making purposeful deformations paved the way for a mathematical use of the Gömböc. As the Gömböc has the minimal amount of equilibrium points for any 3D shape, this means that any other 3D shape can be derived from it. This is analogous to a geometric stem cell, where you can ‘grow’ any shape from the base form that is a Gömböc3.
If the task were only to find a 3D mono-monostatic body (a body with one S, one U and no T points), then it would be trivial. A roly-poly toy would be an example that is also convex. However, the weight below its geometric centre that causes the body to self-right shows that it isn’t homogenous. Another example would be a concave sphere; a section of the material removed from the inside of the top of a sphere would create an unstable equilibrium point at the top, with a stable equilibrium point at the opposing side. This body is homogeneous but not convex. The crux of the task is finding a 3D mono-monostatic body that is both homogeneous and convex. The Gömböc is an object that puts the initial conjecture to rest.
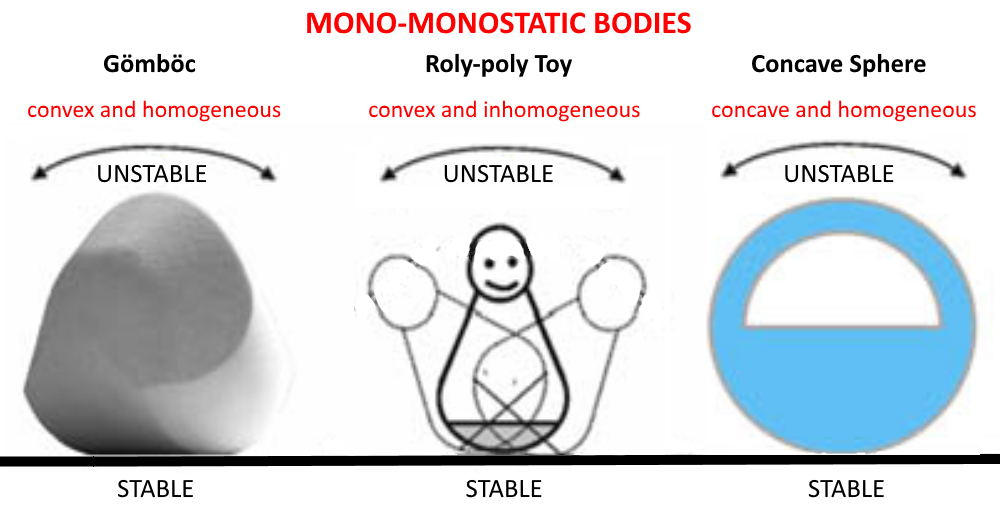
Three types of mono-monostatic bodies
Three counter-examples proved that convex homogeneous 3D bodies were exempt from the limitations created by G (as is the case for 2D bodies) when attempting to find a shape with less than four equilibrium points. The first counter-example shows that a 3D shape can have less than two stable equilibria. The second counter-example shows that a 3D shape can have less than two unstable equilibria. The third counter-example is of a mono-monostatic body, i.e. a hypothetical form of the Gömböc.
The third counter-example only has one stable equilibrium point, one unstable equilibrium point, and no saddle points. Following from the G contradiction in the 2D case, the shape can be split into two parts by a line, one large part and one small part, holding the unstable and stable equilibrium points respectively. G must stay on this line, but G should be on the large side, as there is more mass there. The left sphere on the diagram has a circle as its line: this sphere comes to a contradiction. The right sphere on the diagram has a spatial curve, akin to the curve on a tennis ball: this sphere allows G to stay on the line and be close enough to the bulk of the mass, so there is no contradiction. This proves that a convex mono-monostatic homogeneous 3D body (a Gömböc) exists.
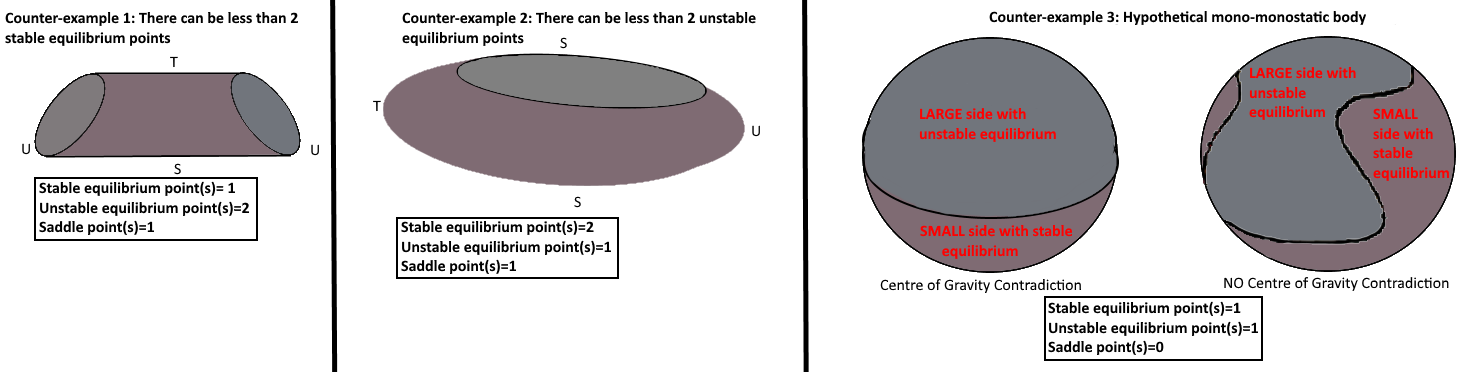
The counter-examples that prove the existence of a 3D Gömböc
There are countless variations of the Gömböc in a geometrical sense, as slight degrees of variation, and other solutions all play a part. But the clear majority are sphere-like. In fact, Gömböc translates from Hungarian to mean ‘sphere-like’. Following this, the researchers wanted to find a Gömböc that was visually distinct from the sphere. The spatial curve (akin to the tennis ball) on the right sphere in the third counter-example paved the way to visualise the now-conventional Gömböc; it gave Domokos and Várkonyi the parameters required to find the distinct solution. This solution appears to look like a pear-shaped object. As it is a convex homogeneous 3D mono-monostatic body, it has only two equilibrium points, but in real life situations the unstable point is near impossible to balance it on, so the object appears always to roll back to the same side, regardless of its initial placed position4.
After the team had discovered the mathematics behind the shape that laid the conjecture to rest, they set in motion an attempt to manufacture a Gömböc. There is a very strict tolerance in the requirements for this: for the sphere-like solutions, the allowed error from ideal to reality is 0.1mm per 10m. This insanely strict tolerance initially hindered their ability to manufacture a prototype; even though state-of-the-art 3D printing technology was used, the first attempt was a failure. Luckily, there is a solution to the Gömböc shape that has a much lower tolerance of 0.1mm per 0.1m, this solution is also distinct from the sphere, and is the main form used to represent the Gömböc. Often it is produced with a light-coloured transparent material, so it readily shows the homogeneity of the body, thus visually proving that the shape isn’t a mangled roly-poly toy in disguise.
Other than from the sophisticated forges of 3D printers, does the Gömböc appear naturally? Yes, and no. Domokos was on holiday with his wife in Rhodes, Greece; whether out of geometrical obsession, or a sly time-wasting ploy, Domokos convinced his wife to join him in analysing the equilibrium points of roughly 2000 pebbles to see if any mono-monostatic pebbles occurred. The search was futile. Nothing appeared, due to the very sensitive and fleeting nature of the Gömböc.
Domokos continued his hunt for a naturally occurring Gömböc-like object, now joined by Varkonyi, they analysed an extensive range of turtles at Budapest Zoo for a year. The team were interested in how turtles can recover from being overturned. Turtles with short shells could use their limbs to overturn, whereas those with high shells were unable to flip over solely through the actions of their limbs. Domokos and Varkonyi were most interested in the turtles/tortoises with the high shells, specifically the Indian Star Tortoise 5.
The Indian Star Tortoise has a shell that’s roughly Gömböc-like. Its advantageous geometry allows gravity to mostly help self-right the tortoise, although, it isn’t a perfect Gömböc – as nature is imperfect – so a little extra bio-mechanical energy from the tortoise’s limbs is required in the self-righting process. The high-dome has advantages such as better thermoregulation, and a better defence against the jaws of a predator. Concerning the Gömböc with its useful mechanical properties, Domokos puts it as “We discovered it with mathematics, but evolutionary biology got there first”.6
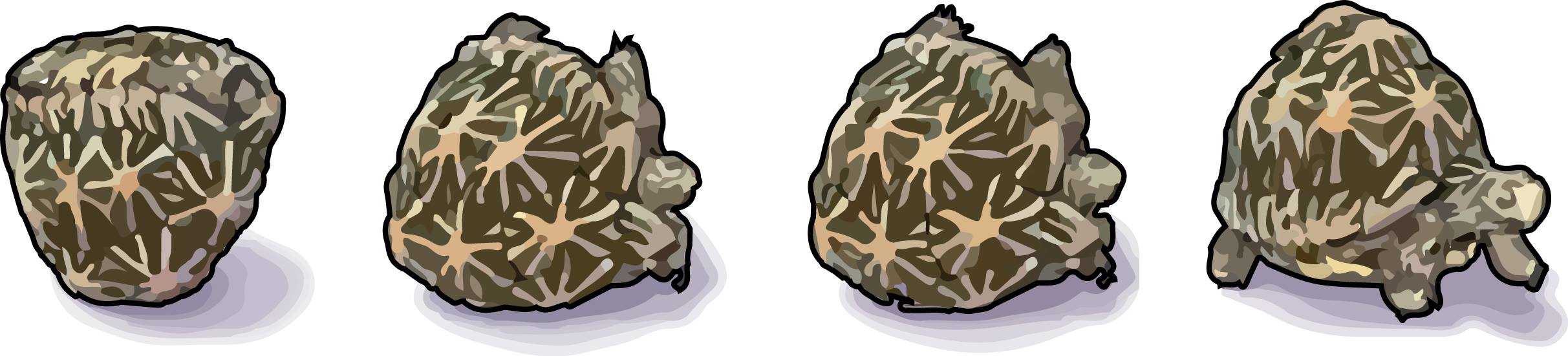
The self-righting process of an Indian Star Tortoise. Credit: Paul Dockery
The level of understanding of biology and mathematics has increased thanks to the Gömböc, but what other practical applications can this shape yield for humanity? In 2015 two developments raised the usefulness of this shape. A renown laboratory at the University of Pennsylvania, deals with the development of helicopter drones, using a Gömböc-inspired exoskeleton that encompasses the top of a miniature drone, the exoskeleton is not homogenous, but its approximation to the Gömböc shape still retains its unique mechanical properties. The miniature drone can self-right after a collision because of its exoskeleton, which is essential when dealing with swarms of drones, because of the high risk of in-air collisions.7
The second development comes from the need to extract as much useful data from the Curiosity rover on Mars, specifically to learn more about its primaeval rivers. As the researchers lacked the data for the mass of river-bed pebbles- usually needed in the investigation of ancient dried-up rivers- another approach was required. Abrasion tends to reduce equilibrium points on pebbles, with the Gömböc shape being the ideal goal of this process. By studying the shape of the pebbles with the mathematical model that the Gömböc helped to produce, they could deduce how far each pebble had travelled, and thus providing a lucid insight into these rivers from aeons past.8
Realisation of this seemingly esoteric conjecture has created an object that defies our intuition and allows for applications over a remarkably disparate range. For an object that appears to be merely a glorified paperweight, it proves that mathematics is a pillar of science that pulls back the curtain of our constricted common-sense revealing the underlying mathematical nature of reality. With nature demonstrating to have found uses of this shape long before we have, the fable of the tortoise and the hare stands accurate. The tortoise seems to have won yet again: in this race to find a mind-bending form.
This article was specialist edited by Timothy Revell and copy edited by Katrina Wesencraft.
References
- Base information behind the Gömböc https://plus.maths.org/content/gomboc-object-barely-exists
- Mathematics behind the contradiction http://www.gomboc.eu/site.php?inc=0&menuId=8
- Information about equilibrium point configurations https://plus.maths.org/content/story-goumlmboumlc
- The article published by the discoverers http://www.gomboc.eu/100.pdf
- The discoverers paper in relation to tortoises http://rspb.royalsocietypublishing.org/content/275/1630/11
- Quote 1 http://www.nytimes.com/2007/12/09/magazine/09selfrighting.html?_r=1&ref=magazine&oref=slogin
- Information related to drones http://www.gomboc.eu/site.php?inc=0&menuId=12&hirId=57
- Information related to ancient martian river-beds http://www.gomboc.eu/site.php?inc=0&menuId=12&hirId=58











The links to the Gomboc website do not seem to work. The correct links are here:
Mars:
http://www.gomboc.eu/en/site.php?inc=&menuId=12&hirId=58
Drones:
http://www.gomboc.eu/en/site.php?inc=&menuId=12&hirId=57
Math:
http://www.gomboc.eu/en/site.php?inc=0&menuId=8
Thanks for flagging this!