A strange world of numbers

 

Integers, as we studied in primary school, are sequentially arranged as -1 ,0, 1, 2. As we moved to higher grades, we encountered rational numbers (fractions). Then, as we zoomed into a sequence of rational numbers, we encountered numbers that cannot be expressed as a fraction (irrational). This collection of rational and irrational numbers creates the number system we all know: real numbers, also known as Archimedean numbers.

Mathematicians also came up with another way to fill in the gaps between the rational numbers: p-adic numbers! P-adic numbers are an infinite collection of numbers associated with a unique prime number ‘p’: the 2-adics, 3-adics, and so on. Just as one can arrange the real numbers based on the distance between them, p-adic numbers are arranged using the p-adic distance. The p-adic distance between two numbers and is defined as the inverse of the distance between real numbers x and y. For example, in the case of 3-adics, the numbers 1 and 4 are at a distance apart, whereas 1 and 10 are at a distance apart. Hence, the numbers that are closer to each other differ by a large power of 3^[1].

This scheme is illustrated in the figure below, where we see that numbers 1 and 10 are in the same circle, emphasising that they are closer than 1 and 4. This idea is counterintuitive to what we have seen in real numbers, but it follows all the rules of the number system.

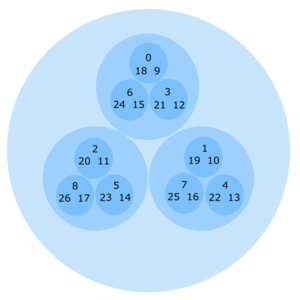
An illustration showing the arrangement of numbers from 0-26 based on their 3-adic distance. Inspired from ^[1].

Superficially one might wonder what good would such a scheme of ordering numbers provide. But p-adics are highly celebrated in the mathematical society for solving various polynomial equations. For example, finding out if the polynomial has rational solutions is hard, however, it is relatively easy to find p-adic solutions^[2].

The main motivation of this article is to let the readers know that there exists a different world of number systems that is counterintuitive from what we have learnt in high school. This Snippet itself does not explain p-adics completely. To learn more about them, you can listen to the 2018 Field Medal lecture^[3] by Peter Scholze of the University of Bonn. This abstract concept is still being explored across various fields, including quantum communication theory in physics.

 

[1] https://blogs.scientificamerican.com/roots-of-unity/the-numbers-behind-a-fields-medalists-math/

[2] https://www.quantamagazine.org/how-the-towering-p-adic-numbers-work-20201019

[3] https://www.youtube.com/watch?v=7xD_JIJj22Y

 

Edited by Hazel Imrie

Copy-edited by Rachel Shannon