Mathematical Knots: It’s Not What You’d Expect

Ever wonder why your earphones tangle to the point where it seems as if they’re trying to stop you from listening to music? Most people would see this as a frustrating test of dexterity, but for the mathematician it’s the real-life manifestation of a field that is still the focal point of research to this day: knot theory.

The fascination with knot theory kickstarted in the 1860’s, when the predominant ideology was that a mysterious substance called ‘ether’ permeated the entire universe. Scottish physicist Lord Kelvin hypothesised that each element is just a distinct knot in the fabric of the ether, and this sparked a flurry of tabulation and research into the field from physicists and chemists alike. When this hypothesis was found out to be false — as the true model of the atom was discovered — interest from physicists and chemists died off, but mathematicians continued their investigations just for the sake of discovery¹.

This echoes Einstein’s use of non-euclidean geometry (geometry of curved surfaces) for his theory of relativity, as the mathematics were developed prior to any apparent real world use. Skip forward to the 1980’s and knot theory had found an application: biochemists discovered that DNA unknots and knots itself using tailor-made enzymes. Understanding this complex process can further our knowledge in gene mutation. Cryptography, statistics and quantum computing all utilise aspects from knot theory, with developments in the field often occurring as a by-product from research into quantum physics. More recently, the interest from chemists has returned as knotted molecules hold great promise for new materials with potentially far superior properties. Chemists work with the same atoms and molecules that comprise knottable DNA, but it is still a formidable challenge to create knots on the atomic scale. These examples demonstrate that mathematics is a universal language of the physical sciences.

To be clear, there is a difference between the knot we’re all used to — the ominous twist in a string or wire — and the mathematical knot. Think of the mathematical knot as a piece of string (with no thickness) that has had its two ends glued together. The simple loop is called the unknot or the trivial knot, and the trefoil knot is the simplest non-trivial knot – it’s the classic overhand knot with its ends glued together.

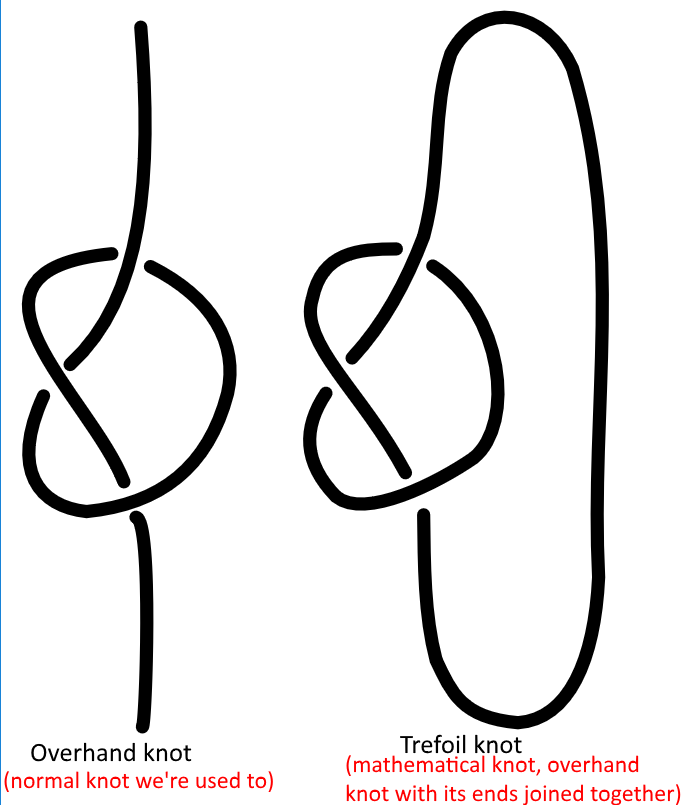
Visualisation as to how the mathematical knot and the ‘usual’ knot differs

We all know from experience that the same problem can come under many different guises, and the same applies to knots. Consider the unknot: versions of it can look like a convoluted tangle but it can always untie back to the standard version of the unknot, even if it takes a lot of manipulation to achieve this. We call each version of a knot a ‘projection’ of the knot. Its projection may vary in the number of crossing points, for example, but it will always be the same knot. This raises an issue: how can you be sure any given knot isn’t the unknot in disguise? We could mangle a knot for hours without any hope of untangling it, but maybe it’s a case of a flaw in our method. A proof is required to show that there are non-trivial knots and we shall elaborate on this proof later. The three Reidemeister moves (R1-R3) can be used sequentially to manipulate knots. They only change the projection of the knot, never changing the distinct type of the knot, as cutting or removing a crossing is forbidden.

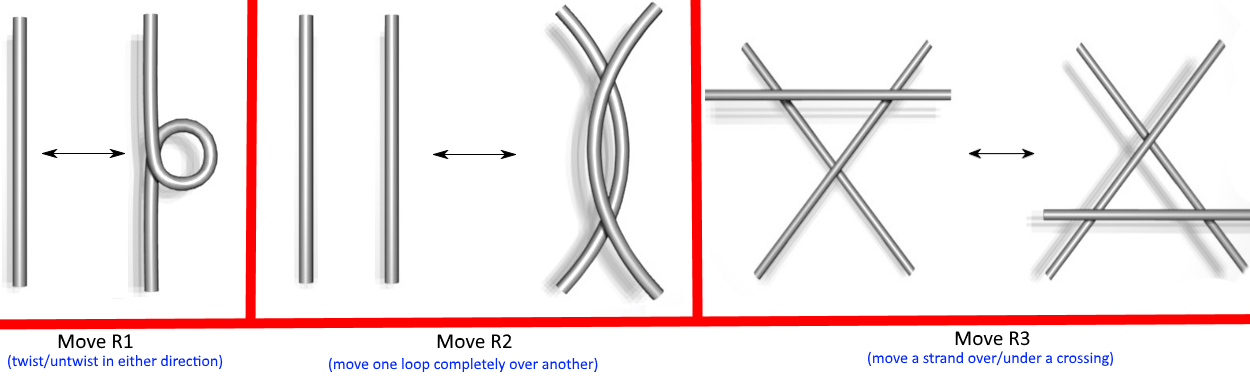
R1: Twist/untwist in either direction. R2: Move one loop completely over another. R3: Move a strand over/under a crossing

The main problem surrounding knot theory is how to systematically distinguish one knot from another. To attempt to distinguish knots we need knot invariants, which is a certain quality of the knot that remains constant regardless of what projection it is in. We’ll see that some invariants are only useful to a degree, whereas the more advanced invariants can cover a vast portion of the knots we know of. As it stands, nobody has invented an invariant that can weave all known knots into a single underlying construct, even though recent developments in the field have attempted to solve this problem.

A basic invariant is the crossing number, the minimum number of crossings that any projection of a particular knot can have. The trefoil knot from some viewpoints can have more than 3 crossings, but there isn’t a viewpoint (projection) where there are less than 3 crossings. This isn’t the best way to distinguish knots from each other as it can be hard to determine a knot’s true crossing number.

We use ‘tricolorability’ to prove the existence of a non-trivial knot. Tricolorability focuses on the strands of the knot — a strand being a piece of the knot in the projection that goes from one undercrossing to another with only overcrossings in between. A projection is tricolorable if there are at least two colours used in the diagram, and at each crossing there is the meeting of three different colours or only one colour. If there’s a crossing where only two colours meet, then the knot isn’t tricolorable. Reidemeister moves do not affect the tricolorability of the knot, so any projection can determine whether a particular knot is tricolorable or not. With the trefoil knot being tricolorable and the unknot being non-tricolorable this proves that there is, in fact, a knot that is non-trivial. Sadly, the figure-eight knot is not tricolorable even though there are other invariants that prove that it is a distinct knot. Once again, we need to look for another invariant that can fully unravel the mysteries of knots ².

A method to prove that there are non-trivial knots, also it’s an example of a knot invariant

Major developments in invariants often came from people working in quantum physics. They produced the Jones polynomial (an arithmetical expression), which is a very useful invariant that uses an algorithm to build a distinct polynomial for each knot procedurally from each crossing. The Jones polynomial isn’t the complete answer, since sometimes a distinct polynomial will lead back to two unrelated knots. The idea of a knot polynomial has been improved upon so that it can encompass more of knot theory, but it is hoped that a radically different approach called categorification will advance us further in this field. Conceptually, categorification is a nightmare to understand: it works contrary to the normal logic of mathematics. It tries to provide a richer structure to understand the knots rather than use the simplified abstractions of the real world that we usually encounter in mathematics. Once again, though, it isn’t the final solution. Even if all known invariants for two very complex knots are the same we still can’t be completely sure that they’re the same knot; a grander, further reaching structure is required to decide if a knot is uniquely distinct ³.

Even though there are many open questions that plague the theory, it has still facilitated some very advanced recent scientific developments. One of the most recent innovations to utilise knot theory was carried out by chemists who synthesised an 8-crossing knot. Previously, chemists were only able to create the trefoil knot (synthesised in 1989) and a 5-crossing knot (synthesised in 2011). It is one of the smallest and tightest knots ever created, utilising only 192 atoms ⁴. At this scale knotting becomes a serious challenge due to the very limited number of entities they can work with. The hope is that this knotted molecule, when weaved together like minuscule chainmail, will have properties unmatched by any contemporary material. Another recent development is the creation of a knot made of a fluid. Using a knot-shaped plastic mould dragged through water filled with microscopic bubbles, the vortex left by the mould enticed the bubbles into a knot-shaped flow ⁵. The researchers hope that this will provide a way for us to study superfluids — fluids with strange quantum properties that are notoriously hard to image if they have knots. Still, the fields utilising knot theory are yet to realise its full potential.

Our understanding has vastly improved since the days of the ‘knots in the ether’ hypothesis, and it shows that seemingly purposeless mathematics can later find its use in an eclectic range of applications. For those of you still wondering why your earphones consistently find themselves in a convoluted bundle, here is your answer: the longer the wire, the higher the probability it will tangle. This is because there is only one way it can be straight but a mind-bending number of ways it can knot, with movement in your pocket and time allowing these other forms to occur. I took so long to tie up this loose end because it truly is easy to get entangled in distractions.

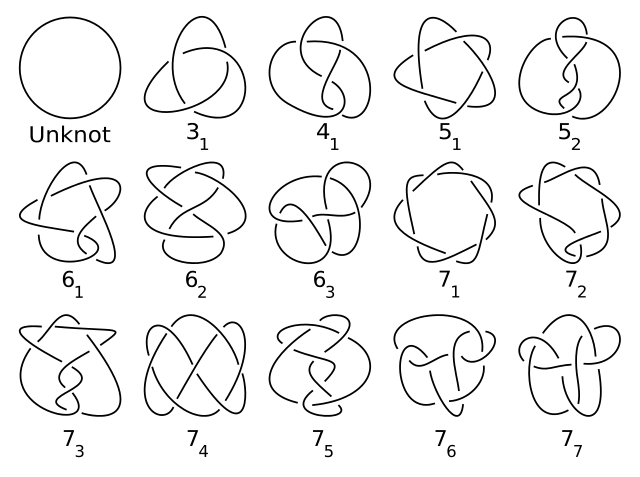
A table of the prime knots (their mirror images have been omitted), these knots can’t be reduced to simpler knots. The first number represents the crossing number (the minimum number of crossing points), and the second number represents the index number of what distinct knot it is with that specific crossing number

This article was specialist edited by Madeline Pritchard and copy edited by Katrina Wesencraft.

1. General knot article https://plus.maths.org/content/why-knot-knots-molecules-and-stick-numbers
2. Tricolorability excerpt https://www.google.co.uk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=2&ved=0ahUKEwi3gNT-hZ7SAhXMDMAKHcC-A24QFggiMAE&url=http%3A%2F%2Fweb.math.ucsb.edu%2F~padraic%2Fucsb_2014_15%2Fccs_problem_solving_w2015%2FTricolorability.pdf&usg=AFQjCNGWA12f8eFWNjgmsmDVHw2VunlS6Q&sig2=VB7gZ2eVWrZrmRFMAp7N8A
3. Information on Invariants https://www.google.co.uk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=4&cad=rja&uact=8&ved=0ahUKEwj3uNqozMzRAhUHPxoKHfzhBXgQFgguMAM&url=http%3A%2F%2Fomlette.irev.net%2Ffiles%2Fprint%2Fknots.ns.pdf&usg=AFQjCNGnj0Dh3nn2D540xbQ8WTeJwMMACg&sig2=VY5cQwm4Deeq1ZkRPXjXPw
4. Article about knotted molecules https://www.newscientist.com/article/2117870-molecules-tied-into-beautiful-octofoil-knot-for-first-time/
5. Article about knot-shaped fluid https://www.newscientist.com/article/mg21729074-500-first-fluid-knots-created-in-the-lab/