What is a Number?

by richardmurchie · January 15, 2017

Image credit: arief hasan via Flickr (CC BY-NC 2.0)

What exactly is a number? We’ve been using numbers at ease for millennia, and manipulating the mental concept of quantity since we inhabited the trees, but not until the past century did the question of its true nature formally surface.

Let’s focus on the number three. The symbol for three (3) can also be the roman numeral III, thus the symbol itself doesn’t shine a light on the true nature of the number. The word for three can also be swapped for the French ‘trois’ which again doesn’t show us anything about its deeper nature. Would you rather encounter three bears or three wolves? It doesn’t matter to the mathematician trying to find out more about ‘three’: quantity is arbitrary in the pursuit of understanding the number itself¹.

However, research into waveforms through Fourier analysis in the 19th century required set theory to advance the field, which set the course for revealing the true nature of ‘3’. A set is a collection of objects in which there is a well-defined way of determining its members; the set notation brackets { } contain the members of a set.

Suppose we have three sets: the five digits of the human hand, the five traditional senses, and every whole number from 1 to 5. We can list the names of the fingers going from the thumb (1), index (2), middle (3) and so on. We can also list the senses: touch (1), sight (2), taste (3) etc. The fatal blow for numbers is that we can replace the corresponding whole numbers with the other set, by counting the digits of the hand against the senses: thumb (touch), index (sight), middle (taste). What this tells us is that counting is merely a one-to-one correspondence against a standard set (usually whole numbers).

To understand the nature of a number, we need a unique standard set that has ‘n’ members for the ‘n’th number. In contrast a non-unique set would be one with five members, as it could be either {1,2,3,4,5} or {6,7,8,9,10}. Instead, we need a unique set which means there is only one such set – the empty set satisfies this. The empty set is a strange device: it opens up the possibility of vacuous truth, a logical statement that is technically true yet not meaningful, as it is based on a false premise. It is the set that represents the different species of shark that can fly; it is also the set of instances where I meet deadlines on time. Yet fundamentally it provides the underpinning for a truth that isn’t so empty: mathematics².

Zero is the number that serves as the basis of mathematics; it only makes sense that we should define the rest of the numbers in relation to it. The empty set is a unique set with zero members, often written either as { } or ∅; we can define zero to be the empty set. Imagine the set notation brackets representing the empty box (empty set) in the analogy below, with zero being the empty box as it has zero members. One is the box which only holds the empty box, thus one only has one member. This method of layering empty sets allows the number n to be defined by a unique standard set with n members – and we have reached the definition of a number³.

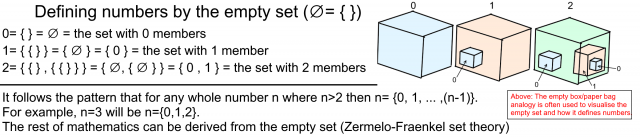
The empty set theory (Zermelo-Fraenkel set theory) that underpins mathematics is important, but mathematics grew organically through gradual developments related to observation and analysis of real-world problems. Although it has evolved into its current rigidly axiomatised form, it does not require the empty set axioms to function as an invaluable tool for our society. That being said, mathematics seems to be a rare school of thought that is truly stronger when it’s built on top of nothing.