No, not the defence headquarters, but its eponym, the five-sided polygon that has been confusing mathematicians for over a century.

Last summer there was a discovery in the field of geometry. This discovery was of the 15th type of pentagon that can tile the plane. ‘Tiling the plane’ means that identical copies of a shape can be repeatedly used to fill a flat surface without any gaps or overlays. This is also called tessellation. Fifteen different types of pentagon can tessellate, but the regular pentagon cannot. So what’s going on here?

Other polygons, such as triangles and quadrilaterals, cooperate with mathematicians on this facet of nature. A regular polygon can tessellate if the internal angle of the shape can divide 360 degrees into a whole number. The resultant integer shows how many polygons of that shape share one vertex. A vertex is a point where two or more lines meet, thus all of the corners of a polygon are vertices (which is the plural form of the vertex). ¹. For instance, the regular triangle has an internal angle of 60 degrees, and so it has six triangles that share one vertex, making the regular hexagon in this process. The regular hexagon also tessellates — bees, with their honeycombs, have been exploiting this for far longer than we have. Yet the pentagon remains perplexing. Regular polygons have sides of equal length with equal internal angles; convex polygons have varying side-lengths and varying internal angles that are all under 180 degrees, with all of their vertices pointing away from the centre. This is where the pentagon fits in, through these 15 convex types, which are distorted relatives of the regular pentagon.

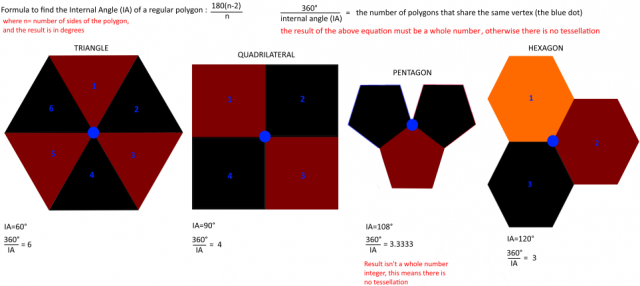
How to find out if you can tessellate a regular polygon, from the triangle to the hexagon.

Don’t be fooled into thinking that these 15 types of pentagon are individual pentagons in their own right. They’re classes of pentagon, described by equations harnessing the relations between the internal angles and side-lengths. This means that each type has degrees of freedom which correspond to variation of angle and length. Although each class has pentagons that belong to no other type, there will be some pentagons that belong to multiple types. Due to each type having degrees of freedom, there are many distinct tessellations that each type can produce.

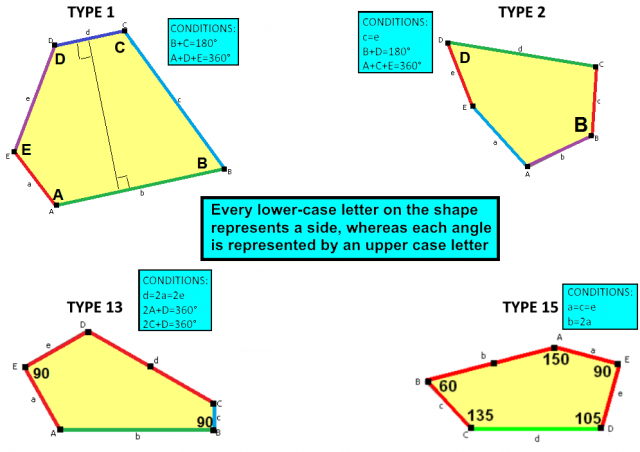
The 1st, 2nd, 15th, and 13th type of convex pentagon respectively in clockwise order, showing the general form of the type and its conditions.

How many convex pentagons in total can tile a plane? This sounds like a simple question, but it’s quite the opposite, since it is related to David Hilbert’s famous 23 unresolved problems that faced contemporary mathematics, posed in 1900. It has been proven that all triangles and quadrilaterals can tessellate. For convex hexagons there was a proof that dictated that there are only three types that can tessellate, with another proof showing that no polygon that has more than six sides can tile the plane. A proof that would put the pentagon to rest does not exist, so there are infinite possibilities for different convex pentagons. There must be infinite types that can tessellate lurking out there, just waiting to be discovered. This is a stinging blow for any researcher that yearns for closure.

Part of one of Hilbert’s problems set down in 1900 was related to this puzzle, but it wasn’t until 1918 that a German mathematician named Karl Reinhardt discovered five types of tessellating pentagon ².The academic community then ignored the problem as they assumed the list was complete. There was no advancement until 1968, when R. B. Kershner uncovered another three types, yet he fell prey to the same trap of assuming the list was complete. In a 1975 issue of Scientific American the puzzle was finally discussed once more, and this time another mathematician, Richard James III, discovered one more type.

Marjorie Rice was a San Diego housewife who had received no formal mathematical education beyond high school. Rice often read Scientific American, and a follow-up article in winter 1975 citing James’ discovery sparked an interest in the pentagon puzzle. Rice constructed her own informal diagram-based notation and procedure to uncover more pentagons, discovering four more between 1976 and 1977 ³. Since she was an amateur and had no formal mathematical training, she was referred to Doris Schattschneider. Schattschneider was a mathematician who had a professional interest in the relation between mathematics and art. She encouraged Rice to continue her work. In turn, Schattschneider formally presented Rice’s findings to the academic sphere. Rice was subsequently honoured at the headquarters of the Mathematical Association of America when one of the distinct tessellations created from her uncovered pentagons was plastered on the lobby floor.

A German graduate student, Rolf Stein, found one in 1985 — then for 30 years there was no progress in the domain, which is surprising due to the computational brute force nurtured over this time period. This streak of stagnation ended when Jennifer McLoud-Mann, Casey Mann, and an undergraduate named David Von Derau, all at the University of Washington Bothell, discovered the 15th type in the summer of 2015. The type was found by a program designed by Von Derau to compute through a large but finite set of possibilities. The search had been in vain for two years, as the results mostly regurgitated either an impossible pentagon or a type that had already been found. But this time it was different — a new type had appeared.

The initial discoverers of the pentagons surely had it easier, as there were an abundance of forms waiting to be found. For instance, if you slice a regular hexagon in half to create two identical convex pentagons, you can use one of the halves to create a pentagonal tiling. Currently McLoud-Mann’s team are modifying the program they initially used to find another type, but when McLoud-Mann was questioned on the prospects of the problem she replied with a distinct pessimism, determining the outlook not to be of closure, but in her words “[to] simply to chip away at the problem” ⁴.

You may wonder, other than the obvious aesthetic aspect that heightens our understanding of the link between mathematics and art, what the practical applications of this endeavour are. As Mann puts it, “[for] those in the maths world, finding this tile is analogous to finding a new atomic particle” ⁵. Scientific fields that can benefit from this include biochemistry (viruses), chemistry (crystallography), structural design, and the emerging field of molecular level self-assembly. Many of the basic building blocks of these pillars of science are determined at least partly by geometry ⁶. A fundamental understanding of how the sum form is produced will advance our knowledge and expertise in these areas.
In essence, this is a discovery of a whole new way nature can assemble itself, and we have no idea if or when the list of tessellating pentagons will come to an end. So here is a word of caution for someone intending to tile their house with all 15 types: make sure you have room for an extension.

This article was specialist edited by Madeline Pritchard and copy edited by Rasa Manda Tamošauskaitė

1. More in-depth mathematical explanation https://en.wikipedia.org/wiki/Pentagonal_tiling
2. Description of the history https://www.theguardian.com/science/alexs-adventures-in-numberland/2015/aug/10/attack-on-the-pentagon-results-in-discovery-of-new-mathematical-tile
3. Majorie Rice information http://britton.disted.camosun.bc.ca/jbperplex.htm
4. Quote 1 http://www.npr.org/sections/thetwo-way/2015/08/14/432015615/with-discovery-3-scientists-chip-away-at-an-unsolvable-math-problem
5. Quote 2 http://www.uwb.edu/news/press/2015/081415
6. Description of some applications http://www.huffingtonpost.com/entry/historic-tile-discovery-gives-math-world-a-big-jolt_us_55d3e39ce4b07addcb4495ba?kv