Erdős Best Served Coded

Gigabytes of interesting, insightful data has been released for public viewing. The file contains never-before-seen information, revealing new knowledge to the world. For the first time in a long time, an introduction like this is not a news story about spying governments and Edward Snowden. There’s been a discovery in the world of mathematics, and it’s massive. Well at least the proof is.

Mathematicians Dr Alexei Lisitsa and Dr Boris Konev of the University of Liverpool have made progress on the Erdős Discrepancy Problem. The pair continued the work of an online collaboration of mathematicians that had tried, but failed, to solve the problem in 2010. The online collaborators had managed to write software to check many different parts of the Discrepancy Problem, but gave up when their technique stagnated. So what is the Erdős Discrepancy Problem?

Suppose that you have an infinite sequence of 1s and -1s, perhaps this was generated by flipping a coin infinitely many times and assigning heads to 1 and tails to -1. What patterns might you expect to see in this sequence? Hungarian mathematician Paul Erdős (pronounced ‘air-dish’, and err ‘Paul’) said that given any number C, it is possible to find a finite part of the sequence*, which when you add all of the elements together, total greater than C. This seems reasonably intuitive yet is incredibly difficult to prove mathematically. This problem has been known since the 1930s, and in 1957 Erdős offered $500 to anyone who could solve it ¹. The $500 have yet to be claimed.

It has been known since the time of Erdős that the conjecture holds for C=1, what Dr Lisitsa and Dr Konev have managed to show is that it is also true for C=2 ². Certainly a step in the right direction, but the proof required was epic. Seriously, epic. To prove the result they used a computer to work out some of the mundane details. Computers are great at, well, computation and so when there are many calculations and possibilities to check computers are well-suited. The problem is that the proof generated takes up 13 gigabytes of data. That’s larger than all, yes all, of the text on Wikipedia. This means that there is no way that a human can check the computer’s results.

No way, you say? 1 gigabyte of data contains 1024 megabytes, or 1048576 kilobytes, or 1073741824 bytes. Each byte contains 8 bits, a 0 or a 1, and it turns out 8 bits is enough to represent a character. So with 1 gigabyte we can store 1073741824 characters. Assuming that our text averages 6 characters per word (including a space), then 1 gigabyte of data is enough to represent 178956970 words, so since we have 13 gigabytes of proof to check, that is 2326440618 words to read. This certainly seems like a lot. If you read 2 words a second, which would be quick to thoroughly understand a mathematical text, for 8 hours everyday, it would take you 110 years to get through the proof.

Part of the reason that this problem, and its partial solution, has received such excitement from mathematicians is the association with Erdős. Erdős is one of the most famous mathematicians in living memory, famed for his vast collection of work and his alternative lifestyle. He wrote over 1500 mathematical articles in his lifetime with over 500 coauthors. Erdős practised mathematics as a social activity. He had no wife, no children and no real home, but always surrounded himself with people. He would arrive at a mathematician’s home and announce “My brain is open.” He would then stay until a few papers’ worth of mathematics was produced and then move on to repeat the process elsewhere ³.

You might wonder, if a mathematician can’t check a proof, whether a theorem has been proven at all. Mathematicians have for some time disputed the philosophical implications of computer-based proofs. This first came to light in the 1970s when Kenneth Appel and Wolfgang Haken proved the Four Colour Theorem using a purpose-built computer program. The Four Colour Theorem says that any map of the world can be coloured in, using only four colours, so that no two neighbouring countries share the same colour. The proof involved checking nearly 2000 cases, and although mathematicians were sceptical at first, it has since gained wider acceptance.

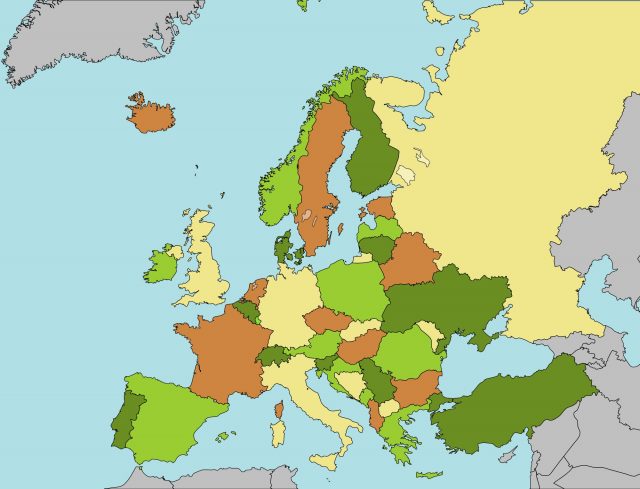
Image Credit: Wikimedia Commons ( License ) A map of Europe coloured using only four colours.

Nowadays many mathematical proofs and theorems have been formalised using computers. There are groups of mathematicians who use computer programs, known as proof-assistants, to help them develop new mathematics. This is a different technique to that used by Lisitsa and Konev, since proof-assistants interactively help mathematicians to prove new theorems, but it uses similar ideas. Computers are unlikely to replace mathematicians anytime soon, since they are only good at computation and not ingenuity, but they are increasingly becoming a valuable part of a mathematician’s toolkit.

Dr Lisitsa and Dr Konev have certainly made progress on the Erdős Discrepancy Problem, but only a very small amount. To truly solve the Discrepancy Problem another proof technique will be required, perhaps using a computer or perhaps not. Either way, for now, the $500 of Erdős remain safe.
*A subsequence is given by choosing elements of the sequence in a systematic way, i.e., every other number in the sequence, or every 3rd number, or every 10th number …etc. We then take a finite number of these and add them up to give the total and ignore the plus or minus sign in the result. This is normally referred to as the discrepancy and hence the name Erdős Discrepancy Problem.

1. http://michaelnielsen.org/polymath1/index.php?title=The_Erdős_discrepancy_problem
2. The paper.
3. Hoffman, Paul (1998). The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. London: Fourth Estate Ltd. ISBN 1-85702-811-2.