Topology: the mathematics of play doh

Topology1 is a branch of mathematics, that emerged very slowly from studies of geometry. However, in the late 1800s and early 1900s, it exploded into one of the largest fields of pure mathematics, a status that remains to this day! The core question of topology is how much can we learn about shapes, spaces, and other mathematical objects by treating them like play-doh (or in posh maths-speak, up to something called continuous deformation).
Continuous deformation (described rigorously through the notion of homeomorphisms) is commonly introduced by giving a sense of what kind of things we can or can‘t do with play-doh. When playing with play-doh, we are allowed to stretch objects, make them larger, flatten them, make them spiky, but they remain the same object. A stretched, big, spiky sphere is still a sphere.
But there is one crucial rule of topology: we cannot change the number of holes in an object. We can’t punch a hole in a disc or glue up the hole in a doughnut. Such moves are “discontinuous”. There is always a point in time where a hole suddenly becomes a not-hole. Keeping track of holes allows us to answer age-old questions such as “How many holes does a straw have, 0,1, or 2?” The answer is 1, since we may continuously deform a straw by squashing it down into a ring, which clearly has just one hole! Also, one cannot find a continuous deformation from the straw into a sphere or a genus (two doughnuts glued together), so it does not have 0 or 2 holes.
Also, we can slowly morph a coffee mug and a doughnut, so to a topologist, they are the same shape! This leads to the well known, great mathematics joke:
Q: What’s a topologist?
A: Someone that can’t tell the difference between a coffee mug and a doughnut.

An example in topology, showing a mug morphing into a donut. Image by Lucas Vieira (CC BY 2.0)
Standard geometry takes into account information like the distance between objects and the size of objects. For a topologist, all triangles are the same. And triangles are the same as a circle. They can all be continuously deformed to one another. So it might seem perplexing how topology can have anything useful to say when objects so obviously different are considered ‘similar’.
One advantage of this approach is that many phenomena in nature change shape continuously; strings of proteins, the sea, leaves, even the shape of our universe itself. Proteins, for example, can get themselves into tangles which make them incredibly hard to identify. However, every tangle results from a sequence of continuous deformations, so using topology, we can untangle them to get a proper look!
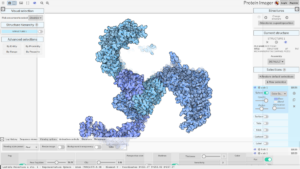
A 3D protein structure. Image by Gianluca Tomasello (CC BY 2.0)
In the same way, topology makes the task of classifying shapes easier by grouping lots of different shapes together via their topological similarities. There are a huge number of 2D and 3D shapes, but not so many if we say it doesn’t matter how many sides a shape has or how big it is, only whether we can continuously deform one into another. It lets us see similarities where, without topology, we would only see differences and untameable complexity.
Topology can help us solve all kinds of mathematical problems where distances and size don’t matter, only the structure of a shape. A classic example is the Seven Bridges of Königsberg2 where it is asked: can you cross all 7 Bridges in Königsberg in one round trip? This problem is considered to be one of the founding problems of topology, and Euler’s solution remains one of the most celebrated papers in all of mathematics to this day.
Crucially, Euler noticed the aspects of the problem which were relevant (the number of islands and bridges between them) and irrelevant (how long the bridges are, or whether the landmasses were mainland or an island). In short, there were a number of continuous deformations (changing the lengths of bridges, for example) that would change Königsberg on the one hand, but end up with equivalent questions on the other. Noticing this led to a general solution by Euler (showing there is no way to make the round trip), and in turn, began the mathematical field of topology.
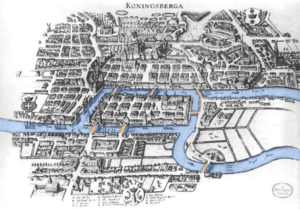
The 7 Bridges in Königsberg. Blue colour represents the river and brown colour represents the bridge. Image by Merian-Erben (CC BY 2.0)
The first course in topology, given by Hausdorff, was rumoured to have had only three students. But now, hundreds of undergraduates attend topology courses every year in Scotland alone. This isn’t just for the sake of mathematical pedantry and the joys of solving puzzles; it’s also because topology is now a vital part of mathematics and science as a whole. Within mathematics, topology has solved several problems, ranging from defining derivatives on complex shapes (differential topology) to the classification of algebras foundational to quantum field theory (K-Theory groups of C* algebras). But even outside of mathematics, topology has found all manner of applications…
1.The topology of knots alone3 has found incredibly broad applications from cancer research to cryptography. In Mario Livio’s book “Is God a mathematician”, he explains how knot theory can be used to describe quantum field theory, a large branch of theoretical physics. When we think of untying a knot, this is a kind of continuous deformation, as seen in the below gif, so it makes sense to talk about them using topology.
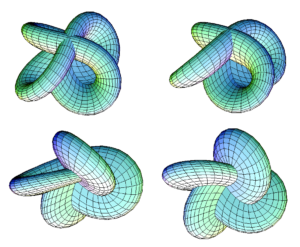
Four different views of the Morin surface by AugPi. Image by Maksim (CC BY 2.0)
2. A branch of topology called persistent homology has led to the emerging field of topological data analysis4. This means that topology helps us detect things like someone hacking into your Facebook account, as well as what kinds of content you might like on tik tok. Using topology, we can group data sets that look similar and notice outliers.
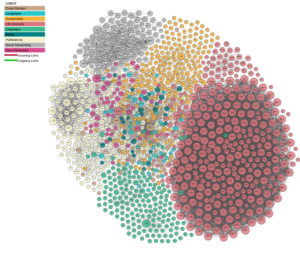
Four different views of the Morin surface by AugPi. Image by Andrejs Abele, John P. McCrae, Paul Buitelaar, Anja Jentzsch and Richard Cyganiak (CC BY 2.0)
3. Configuration spaces have found applications in robotics5. A key thing we use to analyse topological spaces is the paths we can take inside them. The mathematics behind this has proved completely essential in motion planning for robots– knowing how to move around objects or find their way through mazes. Robots use invariants in topology to navigate cave networks, sew together clothes and move around obstacles in a room. These technologies, in turn, tell us more about the natural world we live in, make production cheaper and pave the way for self-driving cars.

Example of an industrial robot. Image by Haophuong21 (CC BY 2.0)
4. In civil engineering, topology has been used to help us build bridges6. Methods have been found that allow us to use far fewer materials to create structures just as strong as before. In turn, this creates greener, more elegant ways to build bridges using topological methods.

The millennium Bridge in London. Image by JJ Jordan (CC BY 2.0)
5. Disruption to muscle fibers can cause stress in the body. Topology has helped us understand which shapes cause stress on our heart, in the process solving a number of life or death problems. This is a huge success of topology. In fact, topology has proven so useful in the study of heart disease that Arthur Winfree claimed that sudden cardiac death is a “problem in topology”7.
MRI of a beating heart. Image by Alith3204 (CC BY 2.0)
In short, one of the largest and least known areas of mathematics appears at first to be child’s play but ends up solving some of the most pressing issues of science and technology today.
References
- https://mathworld.wolfram.com/Topology.html
- https://www.youtube.com/watch?v=W18FDEA1jRQ
- https://plus.maths.org/content/unreasonable-effectiveness
- https://towardsdatascience.com/intro-to-topological-data-analysis-and-application-to-nlp-training-data-for-financial-services-719495a111a4
- https://www.waterstones.com/book/topology-and-robotics/michael-farber/r-ghrist/9780821842461
- https://link.springer.com/article/10.1007/s00004-005-0020-4
- https://www.jstor.org/stable/24968904?seq=1#metadata_info_tab_contents






