It’s 3 September 1857. The SS Central America has just set sail from the port of Colón in Panama after a brief stay and is on its way to New York City. The ship is filled with millions of dollars’ worth of gold straight out of the California gold rush. It’s a beautiful day and a great time of year for sailing.

After nearly a week at sea, SS Central America is making good progress and is now heading up the east coast of the US, when, all of a sudden, the weather starts to turn. A storm is brewing and there is nothing that SS Central America can do about it other than just try to ride it out.

As the hours pass, the storm turns into a hurricane. The wind picks up so much speed that it splits the ship’s sails wide open. Waves smash into its wooden hull and water surges onto thedeck, breaching the interior. The engine becomes so waterlogged that it no longer works, leaving SS Central America completely powerless.

After three days of being pulled along in the eye of the storm and pummelled from either side by the wind and the waves, the ship can’t take any more. Captain William Lewis Herndon knows it is only a matter of time before his ship will suffer a fatal blow that will sink it and so orders the flag to be flown upside down to signal distress and emergency flares to be fired into the sky.

Miraculously, two ships eventually see the signal and come to help, but too much damage has already been done. On the evening of 12 September 1857 one wave too many clatters into SS Central America, bursting open the ship’s timbers. The wood growls before shattering into hundreds of pieces, water surges into the ship and begins dragging it below the surface. Around a quarter of the ship’s passengers were rescued, but the rest, including the captain, tragically went down with the ship. SS Central America, battered, bruised and ultimately beaten, sank to the bottom of the ocean, thousands of metres below the surface, off the coast of North Carolina.

The shock of the loss of life filled the newspapers of the day and was one of the worst American sea tragedies in history. But as time went by people started to wonder about the huge quantity of gold hidden within the remains of the ship on the ocean floor. In the years that followed, many people would dream of finding the SS Central America and claiming its golden treasures. Its notoriety grew and grew, as the quest of finding the gold became like an old pirate’s tale, but nobody ever managed to track it down. It seemed that the SS Central America would be lost forever, until, that is, modern mathematics got involved.

The mathematics of searching for stuff, brought to you by Larry Stone

In 1968 Larry Stone was fresh out of university, putting his mathematical knowledge to the test as part of a search for a United States Navy submarine called Scorpion. He’d recently joined Wagner Associates as an analyst and was told to fly out to Portugal to help find the missing vessel.

‘I’m surprised that they didn’t throw me overboard,’ says Stone. ‘I was this twenty-five-year-old kid and I was telling these navy captains where to search, and they weren’t too happy about it.’ The search for USS Scorpion was pretty difficult and it took a long time to eventually find the vessel but Stone loved every minute of it.

After USS Scorpion, Stone became an expert in searching for stuff with mathematics by pioneering the field known as Bayesian search theory. The field focuses around a mathematical result called Bayes’ theorem, which allows mathematicians to weigh up different pieces of evidence based on their strength and then rigorously work out the probability that something is true. This could be anything from a computer calculating the probability that a particular email is spam (using pieces of evidence such as ‘dollar signs in subject heading’ and ‘sent by foreign prince’) to whether an online shopper would like to purchase this very book (using evidence like ‘user bought Principia Mathematica’ and ‘user bought Twilight’). And in Bayesian search theory, Bayes’ theorem is used to help find missing objects, including lost treasure.

In the 1980s, an American engineer named Tommy Thompson was keen to start a fresh search for SS Central America. Thompson was as charismatic as he was clever and by the summer of 1987 he had charmed 161 different investors into funding his hunt for the long-lost ship.

Stone was known to be the go-to man for a successful search and so Thompson wasted no time in bringing him on board. Thompson’s team had collected hundreds of different eyewitness accounts and reports from the time of the sinking of SS Central America, and produced a list of every piece of evidence that hinted at the ship’s whereabouts. From the list Stone used Bayes’ theorem to mathematically combine all the information and ran computer simulations to try to work out the most likely location of the shipwreck. Stone then produced a map that covered 1,400 square miles of ocean, split into a two-square-mile-wide grid with each square containing the probability of finding the ship at that location. With map in hand, Thompson and his team began searching the ocean with an undersea robot named Nemo. The map told them where to search first and Bayes’ theorem could be used to update all of the probabilities as they went along and if they found any clues.

The first discovery came when they found pieces of broken china, washbowls and toys lying on the seabed, all dating from the nineteenth century. Thompson and Stone knew that they were on the right track and the anticipation started to build. Then, on Sunday 11 September 1988, Nemo spotted something. The on-board cameras slowly focused, the images cleared and the onlookers gasped. There was no mistaking it: SS Central America had finally been found.

Where did I put my keys?

Put very simply, Bayes’ theorem states that for any views that you hold you should always be willing to use new evidence to update your beliefs. For example, if you believed that all mathematics books were a little dull and then you read this one, you would almost certainly have to alter your view. To paraphrase John Maynard Keynes, ‘When the facts change, I change my mind. What do you do, sir?’

When using Bayes’ theorem your initial beliefs are known as priors, which are then used in conjunction with new evidence to produce new beliefs, which are known as posteriors. This means that spotting Bayesian mathematicians is always easy as you can tell by their posteriors. Ba-doom tssh.

Instead of just writing out Bayes’ theorem I want first to show you it in action, so let’s use the theorem to find something. Many readers with nineteenth-century ships filled with gold will be familiar with the problem of losing one, but simply for variety we shall use Bayes’ theorem to find something else – your keys. Where did you put them again?

You know you have lost your keys somewhere in your flat, but they could be in any of your three rooms: the main room, the bedroom or the bathroom. (Yes, this describes my flat.) From prior experience, you know that there is a 70% chance of finding your keys in the main room, a 20% chance of finding them in the bedroom and a 10% chance of finding them in the bathroom. (And, yes, these probabilities come from personal experience.)

Normally when looking for your keys, you dive right in and start searching. But today you feel your inner Larry Stone calling to you. And so, like all good Bayesian search theorists, you decide to draw yourself a little box:

You know from previous searches that your search success rate is 65%, meaning that the probability of you finding your keys while looking in the right room is 0.65. (And, yes, of course I collect this information, who doesn’t?) With this in mind you begin to look for your keys, starting in the main room. You manage to find a few old coins, several crumbs and the first draft of your book’s Bayesian search theory chapter, but no keys. What should you do next? Search the bedroom? It is the room with the next highest probability, but before rushing into the boudoir you decide to do another calculation. Bayes’ theorem states that since you now have a new piece of evidence, i.e. a failed search, you should update your probabilities.

It’s still possible that your keys are in the main room, but it has become a lot less likely. We know that the probability of a search being successful (if in the right room) is 0.65 and so the probability of the search being unsuccessful is 0.35, calculated by 1 – 0.65 = 0.35. This means that the probability of your keys being found in the main room and your search not locating them is given by:

 

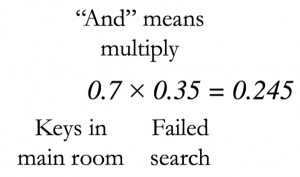
Intuitively, this makes sense. You have already looked in the main room, so it now must be less likely that you will find your keys there. Your posteriors have changed, so you can begin to draw yourself another box:

You’ve so far only updated the probability of finding your keys in the main room, but not yet touched the probabilities of finding your keys in either the bedroom or the bathroom. As the main room is now less likely to contain your keys, the probability of finding your keys in the other two rooms must increase. We know for certain that your keys are in the flat somewhere, and so the three probabilities in the table should add up to 1. To make this adjustment we simply divide each number by 0.545 (which is 0.245 + 0.2 + 0.1), and pop it in the table.

Notice that, as expected, all three probabilities now add up to 1. Surprisingly, even though you have already tried searching the main room, your keys are still more likely to be there than anywhere else. By combining the high probability of your keys being in the main room and your sucky search success rate, Bayes’ theorem says to go back and look again. Luckily, during your second look you find your keys under a cushion. As the old saying goes, ‘Your keys are always in the last place that Bayes’ theorem tells you to look’. And as a reward for your discovery, here is Bayes’ theorem in its full glory:

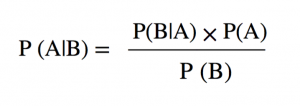
Yes, it’s full of symbols, but considering what we have achieved with it, it’s surprisingly simple and fabulous all at the same time. Let’s just take a moment to appreciate it.

Here’s what the theorem means: both A and B are events and Bayes’ theorem tells us how to calculate the probability of A happening given that we know B has already occurred, which we write as P(A|B). The theorem says that to work out P(A|B), we simply have to multiply two things together and then divide them by something else. The things that we have to multiply are P(B|A), which is the probability of B given A, and P(A), which is the probability of A. Then we divide all this by the probability of B occurring, which is denoted P(B).

If I tell you that the probability of a failed first search in the main room is 0.545, given by adding together the probability of a failed search in the main room, the probability of the keys being in the bedroom, and the probability of the keys being in the bathroom, then the rest is simple. The probability of finding your keys in the main room after one unsuccessful main room search is found by simply plugging in the numbers.

And so using Bayes’ theorem we get 0.45, just as before. Ta-da.

Man vs Bayes’ Theorem

After SS Central America was found, nearly $50 million worth of gold was recovered and sold, but nobody other than Tommy Thompson saw a penny of it. His investors were left without return on their investments, and Thompson went into hiding with a lot of cash. For years nobody knew how to find him. If only there had been some theorem that could have been used to track him down …

Eventually, in 2015, a tradesman tipped off the local authorities and Thompson was arrested at a hotel in Florida. The court case against him is still ongoing, but whatever the outcome he was without doubt part of one of the greatest treasure hunts of all time. Bayes’ theorem isn’t just used for the Bayesian search theory; it can be used almost anywhere where different pieces of evidence need to be put together to make a decision. Bayes’ theorem can play a crucial role in everything from selling books to searching the internet, from spam filters to driverless cars, from medical diagnoses to DNA patterns, from court cases to forensic science, and from online language translators to video games.

Bayes’ theorem can even claim to make companies better, with Bill Gates declaring that the secret to Microsoft’s success is their ‘expertise in Bayesian networks’. And perhaps Microsoft’s most outspoken Bayes’ theorem fan was the legendary (read: annoying) Microsoft Office paper clip called ‘Clippy’.

While popping up and saying ‘It looks like you are writing a letter, would you like some help?’ Clippy used Bayes’ theorem to collect evidence about a user’s behaviour and work out what they were most likely to be doing. Once Clippy was certain enough that it knew what the user was up to, the paper clip could rear its metallic head and offer assistance.

Extracted from Man vs Maths – Understanding the curious mathematics that power our world by Timothy Revell, published by Aurum Press, £14.99 hardback.

(US Link here.)