The Eye of Sauron Galaxy reveals a new way to measure cosmic distances

Recently astronomers have been investigating the “Eye of Sauron” galaxy, also known as NGC4151. It’s a big spiral galaxy and these, like most galaxies, tend to have supermassive black holes in the middle. Supermassive black holes are the largest kind of black holes and tend to be as massive as thousands to billions times that of our Sun. They often collect “accretion discs,” which are mostly made up of dust and gas, or ‘stuff’. This stuff gets stuck orbiting the black hole due to its huge gravitational field. As all this stuff orbits the black hole it is compressed by huge gravitational fields. This makes the stuff hot and as a result the accretion discs glow.
This is particularly interesting for the Eye of Sauron galaxy and not just because the glowing dust is reminiscent of the fires of Mount Doom. It turns out that it’s pretty hard to work out how far away stuff in space actually is. Astronomers use a variety of techniques collectively known as the Cosmic Distance Ladder to work out the distances of far-away objects. So, if you’re trying to measure something close by, such as a planet in our solar system, you can use parallax. Parallax is pretty much triangulation – you measure the position of an object in the sky and you get your friend on the opposite side of the Earth to measure it as well, then you compare and, from the difference and with a little trigonometry, you can work out how far away that planet is.

A composit image of the Eye of Sauron Galaxy captured by the Chandra X-ray observatory, the Jacobus Kapteyn telescope and the NSF’s Very Large Array. Image Credit: Nasa (License)
If you’re looking at something further away, or if you need more accuracy, you can measure the position of your object then wait half a year so the Earth is at the opposite side of the Sun and measure it again. Then, you again have the same trigonometry process to find the object’s position. Of course, you do need to bear in mind that the Earth isn’t the only thing in space that’s moving, so you need to figure out some other details too but this is, more or less, the method.
This will work up to distances of about 100 parsecs (a parsec is ~3.26 light years or 3.086×10^13 kilometers away – for reference our own Milky Way galaxy is 30,000 parsecs across). This is because the position of the stars on the sky has changed by such a tiny amount so that our telescopes can no longer measure it very reliably. On astronomical scales that isn’t very far, so other methods are needed for the next steps on the cosmic distance ladder. For objects further than 100 parsecs away, “Main Sequence Fitting” is used. This utilises the Hertzsprung-Russel diagram (which in my opinion should be called the Hertzsprung-Payne diagram but let’s not go there in this article). This diagram links the spectral type of stars (and hence their temperature ) with their ‘absolute magnitude’. To standardise a star’s brightness, astronomers define the star’s absolute magnitude as a measure of the brightness as it would appear to be if it were at a distance of 10 parsecs from the Earth. There’s a bit of variation for weirder stars but most, while they’re young enough and big enough to be fusing hydrogen in their core, lie along a line called the “main sequence.” So, if you’re looking at a main sequence star and you find its apparent magnitude, which is a measure of the star’s brightness as seen here at the Earth, then along with its temperature and absolute magnitude, you can figure out its size. You do this with a cluster of stars and compare them with stars you know the distance of thanks to parallax. Then you can say, “OK, well I know stars of this size should be this bright, but these ones are a bit dimmer, so they must be further away”, and with a bit of cleverness you can then work out approximately how much further away they really are.
Main sequence fitting is good to about 10,000 parsecs but, well, space is kind of freakin’ huge. So that’s not enough. When this starts failing it’s time to look at a kind of star call a Cepheid variable. Cepheids are useful because they change their state between large and bright and small and dim. They are stars that were unusually massive and hot – stars like this used up their hydrogen fuel very quickly, leaving lots of helium behind, which can sometimes leave them in this pulsating state. The period of pulsation is related to the star’s absolute luminosity so, if you find one and you want to use it to measure distances all you need to is measure the pulsation period and the luminosity, compare this luminosity to that which you would expect for a star of that period and note that if it’s fainter it’s further away, but if it’s brighter it’s closer. You just need to calibrate this against the previous steps of the cosmic distance ladder and you’re done.
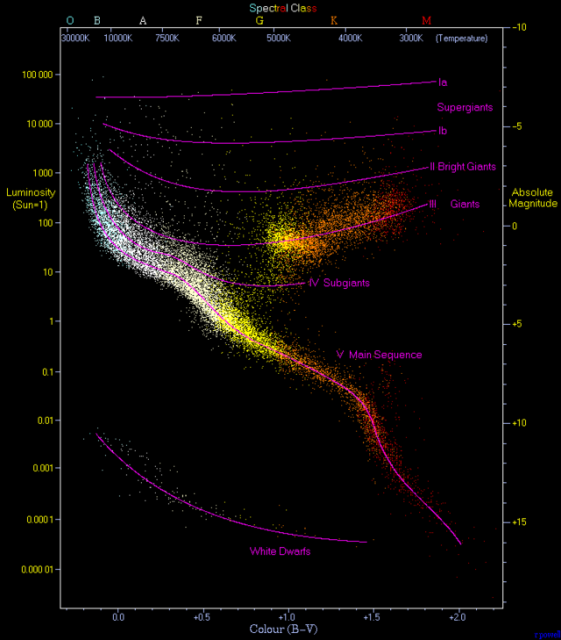
The Hertzsprung-Russel Diagram shows the link between the absolute magnitude of stars and their spectral type. Image via Wikicommons (License)
This will work up to around 15 million parsecs. I suspect you see where I’m going with this, though, and it’s one of the reasons why astronomy is so difficult and why it’s so impressive. The edge of the observable universe is about 14 gigaparsecs away. That’s 14 billion parsecs. 15 million parsecs will almost get you to the next galactic cluster; the Virgo cluster. Incidentally, as we take more steps up this cosmic distance ladder the uncertainties increase because each rung is calibrated against the previous one and so the errors in the calculations add up quickly.
The next step is studying supernovae. One particular type of supernova, imaginatively named Type 1a, is useful for distance measurements. For a Type 1a supernova to occur you need a white dwarf star in binary orbit with another, less dense star. White dwarfs are very small and very dense – like if you squashed The Sun down to the size of The Earth. Because the white dwarf is so much heavier, it strips matter from the companion star as they orbit and thus it steadily gains mass. Eventually it gains enough to reach a tipping point and it becomes unstable and undergoes a runaway nuclear fusion reaction; it “goes supernova.” This tipping point is always the same – anything that reaches this mass will do this. So, once again, you know the mass of the star and you know its brightness so you can figure out its distance.
Cephied variables and Type 1a supernovae are known as “standard candles” because of their regular, predictable behaviour and they’re extremely useful. However, as mentioned earlier, accuracy is a problem at greater distances (supernovae will get you to 200 million parsecs, for those paying attention). To improve the accuracy of distance measurements astronomers need more ways of measuring the same distances so that they can compare them to each other.
This (yes, finally) is where the Eye of Sauron comes in. Remember it has that glowing accretion disc? Well, it’s kind of small (at least, small to be measuring it’s size when it’s so far away) but astronomers at the universities of Copenhagan and Southhampton did something a bit clever 1. They went way back to parallax but looked at the galaxy using the two 10 m dish Keck telescopes in Hawaii. Bigger dishes make for more sensitive telescopes and by combining the light gathering power of both telescopes the researchers achieved an effective resolution equivalent to one telescope with a perfect 85 m diameter mirror. This allowed them to measure the size of The One Ring (ahem… the accretion disc).
The next step was to notice that the dust closest to the black hole was hot enough to emit light in the energetic ultraviolet (UV) and visible parts of the spectrum. Further away, at the edge of the disc the dust was much cooler – it absorbs this radiation and gets hot, so it re-emits the light in the less-energetic infrared (IR) part of the spectrum. It takes some time for the ultraviolet and visible light to get that far and, well, it’s light, so it must travel at light speed. Since distance = speed time, all they needed to do was watch for some stand-out activity in UV near the centre of the disc, then wait for the corresponding stand-out activity in IR near the edge – the time they waited, multiplied by the speed of light, gives the distance across the disc.

The twin Keck telescopes on Mauna Kea in Hawaii. Image via Wikicommons (License)
So, you’ve got the apparent distance across the disc thanks to measurements with the Keck telescopes and you’ve got the absolute distance thanks to light travelling across the disc. Plus, you have the brightness of the disc so, as with all the cool tricks that have gone before, you can figure out the distance to the Eye of Sauron. This new technique has seriously improved the accuracy of this measurement. Before now, the Eye was believed to be between 4 and 29 Megaparsecs away – now we know it’s 19 Megaparsecs away. Combine that with the hope that astronomers will be able to apply this technique to many other spiral galaxies and it gets quite exciting. Knowing the distance to far away objects isn’t only about insisting upon more and more precise measurement – it tells us about the size and age of our universe.
However valuable and fascinating as that is I hope I’ve persuaded you that it isn’t easy. Astronomers are always adding to and improving upon existing techniques and leaps forward like this can take years of research. As a wise man once said, “one does not simply walk into Mordor.”
Specialist edited by Graham Kerr.